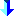|
|
| (1) Posted by Joost de Heer [Thursday, Jun 11, 2009 11:35] |
Andernach 2009 judgement
The judgement for the theme tourneys from Andernach 2009:
http://sanguis.xs4all.nl/chess/andernach2009.pdf
|
|
| (2) Posted by Harry Fougiaxis [Thursday, Jun 11, 2009 11:46] |
Forbidden - You don't have permission to access /chess/andernach2009.pdf on this server.
|
|
| (3) Posted by Joost de Heer [Thursday, Jun 11, 2009 13:29] |
Fixed.
|
|
| (4) Posted by Joost de Heer [Thursday, Jun 11, 2009 17:57]; edited by Joost de Heer [09-06-11] |
A post-Andernach triviality:
JdH
 (= 15+13 ) (= 15+13 )
SPG 7.5, Madrasi (C+)
Threefold theme, 'colourblind' homebase. But there isn't much Madrasi-play, apart from the route of the black knight.
1. Sf3 Sa6 2. Se5 Sb4 3. Sd7 Sd5 4. Sb8 Bh3 5. gh3 Sf4 6. Bg2 Sh3 7. Bb7 Sg1 8. Bc8
|
|
| (5) Posted by Harry Fougiaxis [Monday, Jun 15, 2009 11:19] |
I guess you were there, so you may know. Were any feenschach issues distributed during the meeting? Is the magazine still alive?
|
|
| (6) Posted by Ivan Antonov [Monday, Jun 15, 2009 14:11] |
I've sent my original to Hans Gruber for publishing in "feenschach", and he didn't say a word about closing the magazine.
|
|
| (7) Posted by Michel Caillaud [Monday, Jun 15, 2009 18:36] |
I asked bernd ellinghoven in Andernach if I should pay my subscrption and he took my money. So he looks sure he will go on publishing the magazine
|
|
| (8) Posted by Steven Dowd [Monday, Jun 15, 2009 19:34] |
I am always seeking clear examples of fairy themes, since they don't come to me easily and I must say that the hs#2,5 bicolores by Avner and Caillaud made both the hs# and the bicolores stipulation very clear, and struck me as textbook examples. I think the use of fairy stipulations without fairy pieces made this one good for explaining both stipulations to a rockhead like me. :)
Good work, gentlemen.
|
|
| (9) Posted by Frank Richter [Tuesday, Jun 16, 2009 13:37] |
My latest feenschach issue is labeled with "Summer 2007". Whether there will be newer issues or not in future, the level and the reputation of this journal have significantly decreased for the last years. That is a pity, surely, but it is basically the "merit" of the editor.
|
|
| (10) Posted by Michael McDowell [Tuesday, Jun 16, 2009 14:32] |
How does a judge treat a problem published in "Summer 2007" (I presume in reality sometime in 2009) if it is anticipated by a problem published in another magazine in 2008? Common sense says the 2008 problem is the forerunner, but years down the line people might not be aware of the incorrect date and the earlier problem could lose its priority.
This sort of extreme backdating shouldn't be allowed.
|
|
| (11) Posted by Joost de Heer [Tuesday, Jun 16, 2009 15:11] |
QUOTE
How does a judge treat a problem published in "Summer 2007" (I presume in reality sometime in 2009) if it is anticipated by a problem published in another magazine in 2008? Common sense says the 2008 problem is the forerunner, but years down the line people might not be aware of the incorrect date and the earlier problem could lose its priority.
Not just common sense says that the 2008 problem is a forerunner, see http://www.sci.fi/~stniekat/pccc/codex.htm#27.
|
|
| (12) Posted by Steven Dowd [Tuesday, Jun 16, 2009 17:07] |
Certainly other types of magazines that have this problem (some literary magazines may not publish for a time, for example, due to lack of content) deal with it in a better way. If the magazine is going to have this sort of erratic publication, perhaps volume numbers with the actual date of issue would make more sense. People could subscribe not for the year, but for a volume which would be a year's worth of issues no matter when they appeared.
|
|
| (13) Posted by Sarah Hornecker [Tuesday, Jun 23, 2009 16:47] |
I got official confirmation of bernd ellinghoven that feenschach is continued. He is preparing next issue at the moment.
|
|
| (14) Posted by Hauke Reddmann [Wednesday, Jun 24, 2009 10:32] |
Hey, it's fairy chess, it's *expected* to be irregular :P
If my memory serves me well, 20 years ago things were
exactly the same way, so don't panic in case of a larger
hiatus. If /be/ starts writing capital letters - THEN panic :P
Hauke
|
|
No more posts |
MatPlus.Net  Forum Forum  Competitions Competitions  Andernach 2009 judgement Andernach 2009 judgement |
 ISC 2024
ISC 2024 Forum
Forum  Competitions
Competitions  Andernach 2009 judgement
Andernach 2009 judgement