Website founded by
Milan Velimirović
in 2006
18:08 UTC


| |
MatPlus.Net  Forum Forum  General General  Strong similarity? Strong similarity? |
| |
|
|
|
|
You can only view this page!
| | Page: [Previous] [Next] 1 2 | | (1) Posted by Miodrag Mladenović [Friday, Sep 8, 2006 22:41]; edited by Miodrag Mladenović [06-09-09] | Strong similarity?
In May 2006 issues of "The Problemist" Don Smidley reported "strong similarity" between my original published back in September 2005 and Narayanan's problem that won 2nd prize in Strategmes in 1998. I knew this problem before I composed mine but I do not see so strong similarity. Here are both positions:C.G.S.Narayanan
2 pr Strategems 1998
 (= 11+12 ) (= 11+12 )
#3 |
1. d4 3.c4, d4 3.c4, xd4#) xd4#)
1...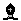 ~!? 2.axb4 ~ 3. ~!? 2.axb4 ~ 3.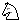 c7# c7#
1...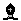 d4!!? 2. d4!!? 2. f1 ~ 3. f1 ~ 3. c4# (2... c4# (2... d4?) d4?)
1...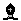 e5!!!? 2. e5!!!? 2. xh1 ~ 3. xh1 ~ 3. xe4# (2... xe4# (2... e5?) e5?)
1...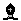 f6!!!!? 2. f6!!!!? 2. g4 ~ 3. g4 ~ 3. e6# (2... e6# (2... f6?) f6?) |
Miodrag Mladenovic
The Problemist 2005
 (= 13+11 ) (= 13+11 )
#3 |
1. xd2#) xd2#)
1...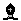 c~!? 2. c~!? 2. e3 ~ 3. e3 ~ 3. h2# (2... h2# (2...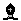 xd2?) xd2?)
1...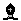 d4!!? 2. d4!!? 2.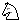 xb4 ~ 3. xb4 ~ 3.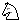 xd3# (2... xd3# (2... d4?) d4?)
1...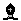 e5!!!? 2. e5!!!? 2. xb7 ~ 3. xb7 ~ 3.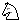 xd5# (2... xd5# (2... e5?) e5?)
1...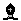 f6!!!!? 2.g5 ~ 3. f6!!!!? 2.g5 ~ 3. g4# (2...f5?) g4# (2...f5?) |
In my opinion problmes are actually very differnt. It's true that both problems are showing "Quaternary Black Correction" theme and somehow it happened that thematic black defenses are completely the same but that's the end of similarity. The position of other picese are completely different. White second moves are also completely different. In my opinion statement "strong similarity" is to harsh. I am wondering what is an opinion of other problemists.
Actually, does anyone know what is definition for "strong similarity"?
| | | (2) Posted by Vlaicu Crisan [Saturday, Sep 9, 2006 08:09] |
I think strong similarity is a very gentle and polite term for partial anticipation.
It is upto the judge to decide the degree of originality of the composition. In your case, the judge might have feel the second white moves are less unified than in Narayanan's problem - it is of course a personal matter of taste.
However, taking in account the presentation (originality of new matrix) and the difficulty of the shown theme, I strongly believe this problem would have deserved a recognition.
Let's see what the FIDE Album judges will say!
| | | (3) Posted by Uri Avner [Saturday, Sep 9, 2006 09:15]; edited by Uri Avner [06-10-14] |
The definition of "strong similarity" is to be found in dictionaries. But this is not a semantic question. Luckily I am audience here, not judge. The only thing that would interest me as audience is: am I happy to see Miodrag's work after having seen Narayanan's? The answer is "yes, of course!" For me, it is fascinating to study the different (and similar) ways these two composers have dealt with the same idea and its difficulties (including side variations, threat etc.) It would have been a real shame to miss any of these works! Thank you, Misha, for the opportunity of seeing them side by side.
Uri Avner
| | | (4) Posted by David Knezevic [Thursday, Sep 28, 2006 13:36] |
The most accurate definition of strong similarity is just that: "a strong similarity" :)
Misha asked a simple question, the simple answer to which he already knows. Despite how polite I want to be, and despite all original details I noticed analyzing Misha's realisation, I cannot put my head in the sand and supress a never-fading feeling of 'a strong similarity'.
Misha, your problem is great, but I'm sorry, I can't help feeling... you know :((
| | | (5) Posted by Hauke Reddmann [Tuesday, Oct 10, 2006 17:03] |
Quote Avner:
"For me, it is fascinating to study the different (and similar) ways these two composers have dealt with the same idea and its difficulties (including side variations, threat etc.)"
Couldn't put it better myself!
I can only add the relevant option (mine :-) :
Just compare my SCHWALBE 7589 (see my homepage,
http://www.hackerhost.info/hosting/user/Hauke/problem2.html)
with that of L.Salai (seen as anticipation by the judge)
(http://www.hackerhost.info/hosting/user/Hauke/version.html).
Exactly the same case - the abstract theme can be termed
identical, the setting is completely different. (Even more
different than in the case here.)
If I were judge, I would quote the anticipee but not
outright throw the problem right out of the tournament.
Hauke
| | | (6) Posted by Miodrag Mladenović [Tuesday, Oct 10, 2006 22:58] |
Thanks everyone for opinion. After all comments it looks like "strong similarity" terms stands as it's stated originally. However personally I still think that there is no so much similarity. How it looks to me there is more similarity in #4 Babson task problems (any two of them) then here. In "Babson" task fourmover first black move is always promotion by black pown on the same square and white 3rd move is always promotion by wP to the same square. However I never saw any comment that there is strong similarity between two #4 Babson tasks (of course unless there is direct anticipation in matrix). In my threemover the only move that is repeated is defense by bB (black defense). Everything else is different.
Hauke, I looked your #2 problem and Salai's one. Personally I do not see any similarity but that's me. I guess everyone has their own view on similarity. By the way it's very good problem. You may want to put it in "Show me your problem" group. I'd like to see more problems there.
| | | (7) Posted by David Knezevic [Tuesday, Nov 28, 2006 21:22] |
Just received new "The Problemist" (Nov. 2006) which, among other interesting material, brings the article "Correction Revisited" by John F. Ling, and saw for the first time this magnificent task:
P. F. Copping
4.Pr The Problemist 1967
 (= 14+9 ) (= 14+9 )
#3 |
1.Qb6:! (~)
1... B~(h2) 2.Rd2:
1... Bf2 2.Qg6
1... Be3 2.Qh6
1... Bd4 2.Qb5:
1... Bc5 2.Qc6
1... Bb6: 2.g8S
6th degree!!! |
Strange, but I didn't know of this problem before although I payed attantion to theme and to author's name since the first quarternary correction in a threemover was also by P. F. Copping (No. 227 in "Chess Problem: Introduction to an Art" by Lipton, Matthews and Rice, 1963). Perhaps the desperate key prevented the problem from deserved quoting over and over again. But there is a point where the aesthetic principles must withdraw and allow real art and courage to dominate.
I thought that such gradual approach of BB to BQ was Narayanan's innovation. I still think that his threemover is a great problem, and I would have probably ranked it the same (2nd Prize) even if I had known about Copping's task. However, I would have looked at it with different eyes, I am sure.
It is impressive how after using almost all material for thematic variations Copping resolved the lack of resources by a zugzwang! Duals in side variations are harmless since main theme is so emphasized that everything else is irellevant, including the capture key. Unfortunately, my English is not good enough to describe how humble and small I feel standing in front of such a gigantic construction!
| | | (8) Posted by Miodrag Mladenović [Wednesday, Nov 29, 2006 12:56] |
Besides bad key this is an excellent problem. However I do not see 6th degree. I think this is 5th degree correction. In my opinion you cannot count Bh2 because it's abandoning control of square d4. Other moves are not doing this so technically this is correction of 5th degree. Did I miss something? If you do not consider black errors then it does look like 6th degree correction.
| | | (9) Posted by David Knezevic [Wednesday, Nov 29, 2006 16:05] |
If we agree that the primary error is 'Bishop plays', then the logic is clear. The removal of Bg1 (as on h2) makes the double threat after 2.Rxd2 possible. All higher degree defences correct against this (even 1... Bd4 cutting the line to d5 and preventing the double threat), and each, starting with Bf2, gradually shortens the BQ diagonal thus cumulating and correcting against all preceeding errors and introducing additional one. Now, if 1... Bf2 is secondary defence, simple counting give us the result of 6 for 1... Bxb6. So, 1... Bf2! = secondary defence, 1... Be3!! = tertiary, 1... Bd4!!! = quarternary, 1... Bc5!!!! = quinary, 1... Bxb6!!!!! = senary defence, period. (the word 'senary' I learnt and borrowed from JFL's article, thank you very much!)
John F. Ling has correctly counted this, but he insists on something that is new for me and I think irrellevant. Namely, he claims that black defences (in second move) should be different for each white attempt to utilize previous degree error. For instance after 1... Bd4 both 2.Qg6? and 2.Qh6? are defeated by 2... Bxc3! (the latter also by 2... de1Q/S, but that is accidental). Or after 1... Bc5 tries 2.Qg6?/Qh6? are both rejected by 2... Bxe7! As I understood him, he thinks that these defences should be different. I disagree and think that the fact that black has corrected the error(s) is sufficient, it does not matter how he did it.
| | | (10) Posted by Miodrag Mladenović [Wednesday, Nov 29, 2006 20:30] |
By definition black erros should be repeated. It's not black error to move bishop. The error is to abandon control of square d4. So I still think that this is only 5th degree correction. However it's great problem anyway. As you know I submitted an original #3 for MatPlus couple of weeks ago. In my problem I am claiming that it's only 4th degree correction (quaternary black correction). However if this is 6th degree correction that would mean that my problem is 5th degree correction. But I could not see it. I think that this is one of the issues that everyone has different understanding how it should work. I based my opinion on definition of black corrections by John Rice in his book "ABC of Chess Problems". If this definition is wrong than I may be wrong.
| | | (11) Posted by David Knezevic [Wednesday, Nov 29, 2006 20:56] |
OK, let's try this way:
In position (1) there is no mate in two.(1) (= 14+8 ) (= 14+8 )
#2 (unsound) | (2) (= 14+7 ) (= 14+7 )
#2 1.Rxd2! (and 1.Qxa7!) |
Remove the Bg1 (2) - a random removal! - and now there would be two solutions, but 1.Qxa7 is wrong since by definition of random move Bishop can go back to g1, so random return 1... Bg1! defeats.
So let us deduce:
1. What is the difference between two positions? - Bishop has moved!
2. Is there an error in second position which did not exist before? -Yes!
Conclusion (1+2): Bishop move = error!
I based my opinion on my opinion :)
| | | (12) Posted by Thomas Maeder [Saturday, Dec 2, 2006 13:06] |
Misha:
Thanks for supporting me in my ongoing fight against wrongly attributed black corrections!!
Milan:
Your logical deduction doesn't work (for me) because black correction is a logical connection between *effects* of moves, not between moves themselves; effects such as interceptions, line openings, blocks, unblocks, loss of control of a square or line, gain of control of a square or line etc.
In the strict meaning of the term black correction*, a black defense X which is a correction of another defense Y *repeats* Y's error that allowed White to continue, but *compensates* it with an added defensive effect. Unless X is a refutation, it also has an added error that allows White to continue.
Kipping's problem is magnificent (after the key anyway), but 2.Rd2: works because the black Bishop has given up control of d4 - to say that 2.Rd2: works because the Bishop moved away is simply not precise enough in the context of black correction. The only specific Bishop move that indeed corrects 1.-B~ is 1.-Bd4 which repeats the error of giving up control of d4, but compensates it with the interception of d2-d5. 1.-Bd4 has the added error of blocking d4 for the black Queen; this added error allows 2.Qb5:.
*In a more relaxed, but very widely accepted defintion, X needn't have the exactly same error as Y. It is also acceptable for X to have a different error that in principle would allow the same continuation that Y does in effect allow.
| | | (13) Posted by Uri Avner [Saturday, Dec 2, 2006 15:45]; edited by Uri Avner [06-12-02] |
The preceding debate has brought (back) to me the following thoughts:
"Correction" may prove to be one of those things (like "Time") that you know perfectly well what they are, until you try to define them; then you discover you know nothing...
This doesn't mean that the attempt to define "correction" is insignificant in itself. On the contrary, it may lead to highly interesting theoretical questions and derivations, even if the ultimate definition is to be found only in the Platonic realm of ideal forms...
The definition in John Rice's "ABC" book has been mentioned, but the very first example brought there (p.50) already puts a question mark on the definition itself. There it is:
T. Tikkanen
1st Prize BABY Ty 1960
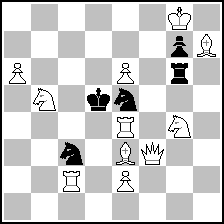 (= 11+5 ) (= 11+5 )
#2
1.Qf8! waiting
1...Sc~ 2.Rxe5#
1...Sxe4! 2.Sc7#
1...R~ 2.Qd6#
1...Rxe6! 2.Qc5#
1...Se~ 2.Qa8#
1...Sc6! 2.Sxc3#
[1...Kc6/Kxe6/Kxe4 2.Qc5/Qf7/Sxc3#]
Question: in what sense is 1...Sc6! "correction"?
Intuitively, everybody feels it must be a correction, but does it obey a formal definition of the term?
| | | (14) Posted by Thomas Maeder [Saturday, Dec 2, 2006 16:32] |
> Question: in what sense is 1...Sc6! "correction"?
Only in a very weak sense.
It is a correction according to the book. 1.-Se~'s error is the loss of control of the diagonal; 1.-Sc6 loses that control as well, but compensates this loss with pre-interception. The added error of blocking c6 allows a new mate.
The problem I have with this kind of correction is that the two effects (control of a line and interception of a line) are very closely related. This is why this kind of correction seems less interesting to me than other kinds, like 1.-Re6:
| | | (15) Posted by David Knezevic [Saturday, Dec 2, 2006 17:00] |
Here we go again...
"Closely related" (!?) - so we came to the point of interpretation. Somebody may feel the close relation between the effects in question, somebody else may not.
And according to what book?
I have a sense of a "Déjà Vu". Thirty years or so ago I was an active participant of similar discussion, my good friend Colin Sydenham may remember our quarrel. Of course, the inevitable result was "agree to disagree" as it could be this time, but the discussion promises to be fascinating and I cannot wait to read more...
Just a short quote instead of my "contributions":
"Milan Velimirovic has described correction as the most beautiful theme in chess problem composition, but its analysis is full of semantic pitfalls and has given rise to many disputes..." (Sir Jeremy Morse, "Tasks and Records" 1995, p.226, §11.12).
I still agree with myself :)
| | | (16) Posted by Hartmut Laue [Saturday, Dec 2, 2006 18:15] |
We must not mix the necessity of a clear-cut formal definition and the invitation to evaluate the contents. The presentation of a black correction may be more or less convincing, but this discussion comes afterwards: First a definition is needed which is an objective one, not subject to matters of taste. What about Milan's proposal with respect to "black (withdrawal) correction"? Remove the black unit (take it off the board with the possibility to move it back from your hand to its square a move later) and look how White will exploit the absence of that unit. Then try to move the unit (on the board) in a way which prevents that exploitation by White. Each move of the unit with this property is a black (withdrawal) correction. With this notion, Tapani Tikkanen's 1.-- Sc6 is clearly a black correction. We may now further discuss if the black corrections 1.-- R:e6, 1.-- S:e4 are of the same character. This is certainly not the case but a different subject. -
Let us apply the same principle to Peter Copping's problem. The mere absence of Bg1 would lead to an irrefutable 3-fold threat by 2.R:d2. Keeping the bishop on the diagonal g1-b6, however, the move 2.R:d2? gives rise to a simple threat only which can be refuted by Black. Compared with the situation with the black bishop in my hand, all these moves are therefore black (withdrawal) corrections (of higher and higher degree, but this is a new discussion).
Logically, it is even irrelevant that the move 1.-- Bh2 is possible. It may be more *convincing* if there is more "arbitraryness" for moves of the black unit in question. But this quality is part of *evaluating* the contents, not simply *describing* it. Therefore, I would even consider all moves of the black bishop as black corrections if there were no square h2. The requirement that there be at least one actual non-correcting variation would already negatively affect the object of the definition, leading to unwanted complications which are better discussed *after*, not *before* the definition. It is much better to not exclude (in the definition) the extreme case that there is no arbitrary move at all. In a second pass we can still discuss if some concrete problem presenting black corrections is successful in the sense of artistically convincing.
| | | (17) Posted by Hauke Reddmann [Saturday, Dec 2, 2006 19:20] |
I fully agree with Hartmut.
@anyone who cares: As the master of wreaking chaos,
I'd like to point to the 117th Thema Tourney of the SCHWALBE,
with the following theme:
1.X (2.Y)
1...z1 2.A#
1...z2 (correcting z1) 2.B#
1...z3 (correcting z2) 2.A#
I don't have to elaborate how this messes around with a "horse-sense"
idea of "correction", right? :-) Thus: Formalization rulez!
Hauke
| | | (18) Posted by David Knezevic [Sunday, Dec 3, 2006 12:11] |
There was a very interesting discussion on REBNORA about that case. Unfortunately, I was not smart enough to download the contents before the discussion board was closed. It would be a pity if it was lost - perhaps somebody has and can provide us a copy? One thing I can promise is that the opinions expressed in this forum will be preserved: the "selected bytes" will eventually be recorded in hardcopy form.
As an illustration of theme similar to one Hauke refers to, here is a problem where it happened as an accident, while I was playing around (though with no successful results) with another theme:
Milan Velimirović
1762. Šahovska kompozicija
1-12/1995
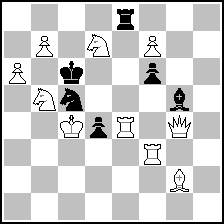 (= 10+6 ) (= 10+6 )
#2 |
1.Rf5 ~ 2.Rc5#
1... S~ 2.Re7#
1... Se4:! 2.Rc5#
1... Se6!,Sd7:! 2.Rd4:,Re6#
1... Re5/Re6 2.b8S#
1... Kd7: 2.fe8Q:# |
There were better problems in Die Schwalbe TT, but I don't have them at hand.
| | | (19) Posted by Vladimir Tyapkin [Sunday, Dec 3, 2006 21:52]; edited by Vladimir Tyapkin [06-12-04] |
Milan, there are quite a few topics exist on the subject of correction from rebnora site thanks to google cache. I was able to find some that may be interesting for current discussion. If you remember keywords, you'll be able to find more.
Tertiary Black Correction
#3 Quaternary Black Correction
a "reversed" correction ?!
| | | (20) Posted by David Knezevic [Monday, Dec 4, 2006 14:08] |
Thanks for a tip, Vladimir. Cached texts need some editting (e.g. diagrams are not shown). I will try to recover what I can, and I invite other members to do so. I will gladly put recovered text on this site!
| |
Read more... | Page: [Previous] [Next] 1 2
MatPlus.Net  Forum Forum  General General  Strong similarity? Strong similarity? |
|
|
|
 ISC 2024
ISC 2024 Forum
Forum  General
General  Strong similarity?
Strong similarity?