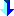|
|
| (1) Posted by James Malcom [Tuesday, Nov 19, 2019 01:52]; edited by James Malcom [19-11-19] |
Try solving this
It's plain and simple-it's White to move and mate in two moves. I dare you to try and solve it!
WTM, #2
 (= 9+3 ) (= 9+3 )
|
|
| (2) Posted by Sarah Hornecker [Tuesday, Nov 19, 2019 02:05] |
1.fg e.p. h4 2.g8R mate
|
|
| (3) Posted by James Malcom [Tuesday, Nov 19, 2019 03:01]; edited by James Malcom [19-11-19] |
Nice job solving Siegfried! But tell me, how does that makes any sense? ;D
:
|
|
| (4) Posted by seetharaman kalyan [Tuesday, Nov 19, 2019 10:32] |
Black has no last move. So it is black to play. However there is no mate in two even if black starts and white takes his two moves. Only way is for the white knight to capture white pawn and mate on b6 !
|
|
| (5) Posted by Vitaly Medintsev [Tuesday, Nov 19, 2019 10:45] |
I think it is a joke puzzle. The last Black's move was Pg8-g6 :-)
|
|
| (6) Posted by Hauke Reddmann [Tuesday, Nov 19, 2019 10:50] |
Mate in 1, Bf7-d5. The bishop is 3 m tall and can
shoot over the horse :-)
(That's the problem with joke puzzles, if the solvers
get creative the joke is on you...)
|
|
| (7) Posted by James Malcom [Tuesday, Nov 19, 2019 14:18] |
Yes Vitaly! But how did it get there?
|
|
| (8) Posted by Vitaly Medintsev [Tuesday, Nov 19, 2019 16:49] |
I don't know.
Maybe Pg7 was scared in the start game-array position and it leaned back, pushing Sg8 off the board :-)
|
|
| (9) Posted by Viktoras Paliulionis [Wednesday, Nov 20, 2019 00:37] |
0.g8=bP Pg8-g6 1.fxg7 e.p.
|
|
| (10) Posted by James Malcom [Wednesday, Nov 20, 2019 01:44]; edited by James Malcom [19-11-20] |
That is correct indeed Viktoras.
|
|
| (11) Posted by seetharaman kalyan [Wednesday, Nov 20, 2019 05:09] |
since anything goes, my solution also correct
|
|
No more posts |
MatPlus.Net  Forum Forum  Twomovers Twomovers  Try solving this Try solving this |
 ISC 2024
ISC 2024 Forum
Forum  Twomovers
Twomovers  Try solving this
Try solving this