Website founded by
Milan Velimirović
in 2006
4:25 UTC


| |
MatPlus.Net  Forum Forum  Helpmates Helpmates  A challenge for solvers: h#5 A challenge for solvers: h#5 |
| |
|
|
|
|
You can only view this page!
| | | (1) Posted by Marcos Roland [Wednesday, Aug 22, 2007 19:10] | A challenge for solvers: h#5
Félix Sonnenfeld used to say this was his most difficult problem to solve:
Félix Sonnenfeld
Die Schwalbe 1966
 (= 3+3 ) (= 3+3 )
h#5
In fact, I think it's a "hard nut to crack". Maybe someone would like to give it a try...
| | | (2) Posted by Miodrag Mladenović [Saturday, Aug 25, 2007 19:20] |
Nice solution but not so hard to solve. It took me about 5 minutes to solve. I'll not give a solution since it's challenge for solvers. However if someone does need some help the first move is to the corner of the board (very nice). There is very nice play so it's very good helpmate moremover.
| | | (3) Posted by Marcos Roland [Sunday, Sep 2, 2007 04:58] |
Thanks, Miodrag, for your comments. In fact, it seems that the solution of this problem is not so hard to find for very strong solvers. As for me, I confess that this problem gave me a severe headache when Sonnenfel showed it to me twenty years ago.
At this point, I’d like to suggest some ideas, maybe to share some ideas, about a rational approach to solve this helpmate. Hopefully these ideas could be helpful, at least for the average solver, in solving some similar longer helpmates. In fact, much of my suggestions comes from an interesting story that Ricardo Vieira told to me about how he demonstrated the solution to the author himself. Ricardo’s reasoning contains 21 points, and I won’t try to expose all of them here. Instead, I’ll mix his entirely logical, mathematical reasoning with some practical considerations.
First of all, let’s see the possible mate positions. Excepting positions with the black king on the border (it seems not to be the case here), we have only three distinct mate positions, and respective echos (of course, the placement of the kings in the positions I give here is arbitrary):
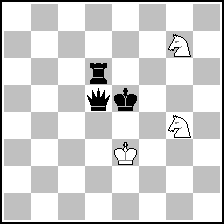 (= 3+3 ) (= 3+3 )
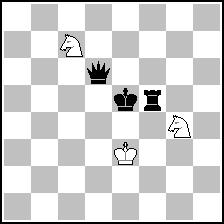 (= 3+3 ) (= 3+3 )
 (= 3+3 ) (= 3+3 )
(Of course, the position of the "second" knight can change in these diagrams: in the first one, the Sg7 could be on d4, etc.)
Two important things to be noted here: i) all the pieces, white and black, are used, with perfect economy; this renforces the “feeling” that the mate occurs in the middle of the board, not on the border; ii) the white knights occupy squares of different colors, as in the set position: that means that the two knights altogether make an even number of moves (4 or 2). This second point is crucial, because we can deduce from it the number of moves made by the white king: 1 (5 – 4 = 1) or 3 (5 – 2 = 3).
Let’s consider firstly if it’s viable a mate position with only one move by the white king. A quick glance to the position shows us that isn’t the case. For instance, if the white king goes to c2, so the black king has to move to c4 or e2: five moves, in both cases, and the queen and rook don’t have time to reach any blockade square.
So, it rests only one alternative: the white king should make 3 moves. In this case, which would be his route? Well, the diagonal path b1-e4 suggests itself (and this is a very practical consideration): a) it goes into the direction of the black king; b) the diagonal route is very attractive both for the composer and the solver, because it involves automatically a unique way of linking two squares with the minimum number of king moves. As John Nunn indicates in Solving in Style, Gambit, 2002, page 113, “If there is no special clue, one should examine diagonal paths first”.
So, we have a very strong candidate square for the white king in the mate position: e4. Accordingly, the black king should go to e6 or g4. We can quickly eliminate e6: the two white knights would need four moves to reach the right squares and they have only two (5 – 3 = 2).
Finally, we arrive to the position with the black king on g4. Let’s put the two kings on the “candidate” squares (e4 and g4), without moving yet the other pieces:
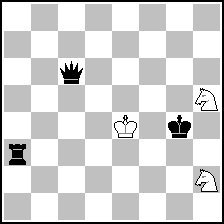 (= 3+3 ) (= 3+3 )
We could continue the “rational approach” further longer, but I think at this point every solver can “see” quickly a mate position which can be reached in the required number of moves:
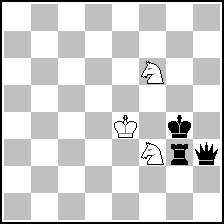 (= 3+3 ) (= 3+3 )
And it's not difficult to find the precise order of moves: 1.Qh1+ Kc2 2.Rg3 Sf3 3.Kf5 Kd3 4.Kg4 Ke4 5.Qh3 Sf6#. That's the solution.
Curiously, the black queen could be on c5 in the initial position (see diagram).
 (= 3+3 ) (= 3+3 )
But in this case, the mate position includes black’s Qg3 and Rh3. Solution: 1.Qg1+ Kc2 2.Rh3 Sf3 3.Kf5 Kd3 4.Kg4 Ke4 5.Qg3 Sf6#.
 (= 3+3 ) (= 3+3 )
| | | (4) Posted by Marcos Roland [Sunday, Sep 2, 2007 20:46] |
In the version with black queen on c5, the white Sh2 should be on g1:
 (= 3+3 ) (= 3+3 )
And the solution goes 1.Rh3 Sf3 2.Qg1+ Kc2, etc. Sorry.
| |
No more posts |
MatPlus.Net  Forum Forum  Helpmates Helpmates  A challenge for solvers: h#5 A challenge for solvers: h#5 |
|
|
|
 ISC 2024
ISC 2024 Forum
Forum  Helpmates
Helpmates  A challenge for solvers: h#5
A challenge for solvers: h#5