|
| Page: [Previous] [Next] 1 2 3 |
| (21) Posted by Hauke Reddmann [Tuesday, Mar 31, 2020 10:19]; edited by Hauke Reddmann [20-03-31] |
Is there a Popeye option to test for this?
 (= 5+5 ) (= 5+5 )
(Almost-working) Example: 1.g4 hxg4. Now
White can lengthen by Bf5. This easily can
be avoided by shifting and leaving "i6"
unguarded. 1.gxh3 g4 2.hxg4 hxg4 3.Be8 -
this can NOT be avoided in the 1.gxf3
line.
|
|
| (22) Posted by Joost de Heer [Tuesday, Mar 31, 2020 12:57] |
QUOTE
Is there a Popeye option to test for this?
begin
fors 6R1/3B4/8/6pp/7k/5p1p/5PPK
stip #1
opt var nothr
twin stip exact-#2
twin stip exact-#3
twin stip exact-#4
end
Which shows that the #4 is dualistic (both gh3 and gf3 work).
|
|
| (23) Posted by James Malcom [Thursday, May 7, 2020 02:56]; edited by James Malcom [20-05-07] |
Here is another 3/4 Albino. The mates are all exact. The only line that is yet to work in the scheme is the #3. If that could be done, then it would be in full.
Mate In 1, 2, & 4
 (= 9+8 ) (= 9+8 )
|
|
| (24) Posted by Zalmen Kornin [Thursday, May 7, 2020 09:32] |
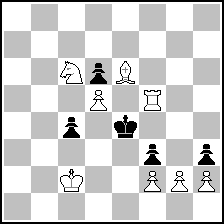 (= 8+5 ) (= 8+5 )
C-
|
|
| (25) Posted by Zalmen Kornin [Thursday, May 7, 2020 09:32] |
 (= 8+5 ) (= 8+5 )
C-
|
|
| (26) Posted by Zalmen Kornin [Thursday, May 7, 2020 09:32]; edited by Zalmen Kornin [20-05-07] |
 (= 8+5 ) (= 8+5 )
C-
(There's some bug here... i shot only once)
|
|
| (27) Posted by Marjan Kovačević [Thursday, May 7, 2020 14:38] |
I liked it, Zalmen, all three times :)
|
|
| (28) Posted by James Malcom [Thursday, May 7, 2020 15:39]; edited by James Malcom [20-05-07] |
Zalmen, I have encountered the same thing. If you press “Submit” two times in a row, it gets posted twice.
And the #3 does not work because after 1. gxh3 c3, there are ways of extending it to a #4 such as 2. Rf5 Kf4 3. h4,Rh4/g1/g3/g6g7g8 Ke4 4. ~#. Such is the problem I had and could not fix.
|
|
| (29) Posted by Hauke Reddmann [Friday, May 8, 2020 11:28]; edited by Hauke Reddmann [20-05-08] |
Quick idea: put the tempo bP(s) on i5. Then i5-i4xh3
kills the guard of g4, so White can't delay his #3
any further (remove the Bc6). You just need the #4
then, by g4 overguarding the R and freeing another
piece. Test, Test:
 (= 13+6 ) (= 13+6 )
If I understand the exact-n# correctly, Popeye says C+!
EDIT:
 (= 10+5 ) (= 10+5 )
Surprise bu^W bishie mate!
SON OF EDIT:
 (= 8+8 ) (= 8+8 )
Now with model and b#1 :-)
Hauke
|
|
| (30) Posted by James Malcom [Friday, May 8, 2020 16:05] |
Hauke, the first two don’t work but “The Son Of Edit” one might. There is only one thing that might ruin it.
In the #3 line, after 1. fxg3 h4 2. Rf5, Black can play either hxg3 or Ke4. If hxg3. then 3. Rf5# is the only option. But if Ke4, then 3. g4 Kd4 4. Rf5 extends the #3 into a #4. Shall the move Ke4 be considered a cook or a poor Black defense?
|
|
| (31) Posted by James Malcom [Friday, May 8, 2020 16:05]; edited by James Malcom [20-05-08] |
BLANK
|
|
| (32) Posted by Hauke Reddmann [Friday, May 8, 2020 19:16] |
No idea - normally short mates don't count as defenses
at all, so that's probably a matter of convention.
As I said, all three have only one solution when
tested with the stipulation exact-n#, and thats what
I relied on.
|
|
| (33) Posted by Joost de Heer [Saturday, May 9, 2020 20:26] |
All three Hauke's compositions are correct.
|
|
| (34) Posted by James Malcom [Sunday, May 10, 2020 03:53]; edited by James Malcom [20-05-10] |
But Joost, the point of the challenge is for there to be a unique mate in 1, 2, 3, & 4 for each pawn move. If a #3 has options to be a #4, then the #4 isn’t unique thus ruining the entire thing. Hauke’s positions are correct directmates yes. but entirely correct not under the challenge.
Hauke’s third problem almost does, hence why I am asking for opinion if in the #3 part if 2... Ke4 cooks it or is considered poor Black defense, thereby keeping the problem intact within the challenge.
|
|
| (35) Posted by Andrew Buchanan [Sunday, May 10, 2020 06:46]; edited by Andrew Buchanan [20-05-10] |
Not got into this exciting Albino task, but there seem to be three possible definitions:
(1) Regular: short mates are totally forgiven. For each n, one key results in mate in at most n moves.
(2) Exact: short mates are totally not ok. For each n, one key results in mate in exactly n moves, in the sense that there is no weak Black play which admits a shorter mate.
(3) Rewan Demontay super-exact. Even longer mates are not ok. For each n, one key results in a position in which all possible Black defences result in a mate in exactly n. Any deviation by White in any line from the plan will result in stalemate, *not* in a longer mate.
Now 3 seems to be what Rewan Demontay is looking for. If not, can he characterize his criterion more precisely. But I think this is extraordinarily hard to deliver. For example, even in Son of Edit, if we look at the #2, after 1. f3 h4, if White does not play 2. Re4# he could still randomly play e.g. 2. Bb1 Kc4, which according to an engine seems to lead to a mate in 7. Does that "cook" the problem?
|
|
| (36) Posted by Hauke Reddmann [Sunday, May 10, 2020 09:57]; edited by Hauke Reddmann [20-05-10] |
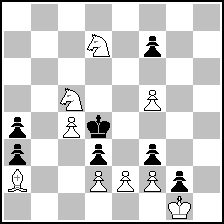 (= 9+7 ) (= 9+7 )
Superexact (no "bad" defenses for Black, since all his moves
are uniquely forced) but of course not superduperexact (all else
than #1234 is not won). EDIT: Unless he insists on a1S. :-)
SUPEREDIT: Or even 1.Kh2 f6 2.e3#, but I'm sure that some h# wasn't what
Rewan meant...
|
|
| (37) Posted by Zalmen Kornin [Sunday, May 10, 2020 10:25]; edited by Zalmen Kornin [20-05-10] |
@Marjan: Nice that You liked, but it would be also nice that someone with admin powers could delete two of the posts...
@ Rewan: I followed the discussions, my point was that there's nothing wrong with the #3 in Your last diagram UNTIL that corresponding step. When we arrive to the last part, then we realize that the #3 can become a #4 if White play against the Chess conventions. Yes, we are already commiting some kind of contravention, because we excluded the #1 and the #2. But against the #3 we cant apply the same procedure, because it can metamorphose itself in a freaky #4. Against the chessical common sense. If we test the diagram I showed with a Chess playing machine the result is C+:
Time Depth Score Positions Moves
0:22 4/11 Mate01 5907654 1.gxf3#
0:22 4/11 Mate02 5907682 1.g3 c3 2.Rf4#
0:22 4/11 Mate03 5907742 1.gxh3 c3 2.Rg5 Kf4 3.Rg4#
0:22 4/11 Mate04 6126908 1.g4 c3 2.Rh5 Kf4 3.g5 Ke4 4.Rh4#
Because under the classical Chess rules a #3 is so to say compulsory, and the public - the ordinary in-the-street Chess lover will exclude the #3 key as he excluded already the #1 & 2. Maybe exact should be presented as a pre-stablished condition (But I also consider and understand Joost's argument that this is already implicit). Even so, i believe that Your 3/4 Albino- 1234 could be presented as
"exact #1,2 and 3 ; (and * #4)" under the diagram I showed. Even so, of course that an exact #1234 is also a classic #1234 - this is undeniable.
***** @Hauke: The examples You presented demonstrate that the "exact" as we know since Hannemann 1933 with his AUW-#1234 can be replicated in an Albino-#1234, and even this newest Rewan's concept of "super-exact" realized. Well done!
|
|
| (38) Posted by Joost de Heer [Sunday, May 10, 2020 10:50] |
No, the #3 line isn't valid for the #4 mate, because black can defend with a line which would lead to a #3, not a #4.
You don't seem to be able to grasp the concept of an exact mate: Earlier mates are NOT allowed. An exact-#3 has no solution if black can defend on his first move with a move which leads to a position with a #1 but not with a #2.
|
|
| (39) Posted by Zalmen Kornin [Sunday, May 10, 2020 11:12] |
The #3 and the #4 are completely separated, that's clear.
|
|
| (40) Posted by James Malcom [Monday, May 11, 2020 02:06] |
Joost, I very well now what an exact mate is. Andrew perfectly described the challenge as being “superexact.” Is it arbitrarily difficult to compose? Yes, yes it is. But sometimes the extremity of a challenge is what makes it fun. Why not create a challenging challenge? An albino with exacg mates in 1, 2, 3, & 4 is rather easy to medium to create, hence why I stepped it up a notch. I do thank you for clarifying the concept of exact mates for the challenge.
And superb work creating a “superexact” albino mate in 1, 2, 3, & 4 Hauke!
|
|
Read more... |
Page: [Previous] [Next] 1 2 3
MatPlus.Net  Forum Forum  General General  Albino & Pickaninny-Mate In 1, 2, 3, & 4 Albino & Pickaninny-Mate In 1, 2, 3, & 4 |
 ISC 2024
ISC 2024 Forum
Forum  General
General  Albino & Pickaninny-Mate In 1, 2, 3, & 4
Albino & Pickaninny-Mate In 1, 2, 3, & 4