Website founded by
Milan Velimirović
in 2006
18:37 UTC


| |
MatPlus.Net  Forum Forum  General General  Chinese Pawns Chinese Pawns |
| |
|
|
|
|
You can only view this page!
| | Page: [Previous] [Next] 1 2 3 | | (1) Posted by Kevin Begley [Thursday, Jan 3, 2013 04:09]; edited by Kevin Begley [13-01-03] | Chinese Pawns
I've studied plenty of fairy problems employing a wide variety of "Chinese units."
I've played Chinese chess -- long ago, I even bought a book on strategy in xiangqi (I vaguely remember flipping through it, before squeezing it into the shelf).
I can even tell you that popeye has a dedicated piece called "Chinese Pawn."
But, I don't know what it is.
I think I've reverse engineered the movement diagram, but my testing wasn't necessarily exhaustive.
If my faded memories of xiangqi can be trusted, I know that this unit does not move (at all) the way I expected it would.
If anyone can please provide me a working definition, I'd be in your debt.
A sample problem isn't necessary, but if you know of a good one, please share that, too.
Thanks.
| | | (2) Posted by Bojan Basic [Thursday, Jan 3, 2013 14:31]; edited by Bojan Basic [13-01-03] |
There is a definition in "Variant Chess" 6, page 73. Chinese pawns are pawns that does not promote, but instead move horizontally when reach the promotion rank.
Here is a sample problem:
Ian G. Richardson
Variant Chess 1991
"Hands Across the Sea"
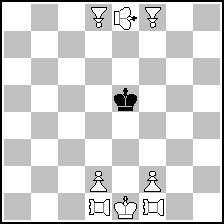 (= 8+1 ) (= 8+1 )
#5 (7+1)
2+0 pao (d1), 2+0 chinese pawn (d8), gold e8
b) remove everything from the row 8 and add crane on e7, #7
(Gold: moves like King, but not diagonally backwards; Crane: moves like King, but not sideways.)
| | | (3) Posted by Kevin Begley [Friday, Jan 4, 2013 07:27]; edited by Kevin Begley [13-01-04] |
Thank you Bojan.
I seem to have derived this unit's movement pattern from popeye, while under the influence of a fairy condition (which I had forgotten to remove).
Aside: When looking for information about these units online, I uncovered indisputable evidence that fairy chess is absurd.
Try to follow the logic of Mayhematics, by George P. Jellis:
A "Threeleaper" is a leaper, like a Knight, but in a {0,3} pattern -- whereas a Knight leaps in a {1,2} pattern.
A "Fourleaper" is also a leaper, but in a {0,4} pattern.
Got it? Good. Right?
Don't ask why we should care about the silly names people invent -- yes, "Leaper{0,3}" is good enough.
The point is this, boys and girls -- guess the movement pattern for the "Fiveleaper."
Ooops. Mayhematics says the "Fiveleaper" has a combination of two leaping patterns {0,5}+{3,4}.
By comparison to the people who named Iceland and Greenland, one set can proudly admit that their convention was based upon ulterior motives.
Which would you rather be: deceptive, or disorganized?
What's the name of the leaping unit with the {0,5} pattern? "Identity-Victim-Leaper" ?
| | | (4) Posted by Bojan Basic [Friday, Jan 4, 2013 15:22]; edited by Bojan Basic [13-01-04] |
Though there are indeed many inconsistencies, I cannot agree that the ones you mention are particularly good examples. Namely, the movement pattern of Chinese pieces (leo, pao, vao...) is derived from the game called xiangqi (a Chinese variant of chess). In that game there is also a piece (called a soldier) that is an analog of a chess pawn, and the movement of the fairy piece Chinese pawn discussed here is actually derived from the movement of a soldier.
It seems to me that your argument about "n-leapers" also misses one point. Namely, "n-leaper" is a piece that may jump exactly n units from the starting square (measured from center to center). That is way threeleaper and fourleaper have only one possible leaping pattern (because that is the only way that puts them exactly three, respectively four squares away from the starting square), while fiveleaper has two possible leaping patterns (in both of them he ends the jump exactly five units from the starting square). A "twenty-five-leaper" would thus have a combination of three leaping patterns: {0,25} + {7,24} + {15,20} (of course, this makes sense only on a large board) and, e.g., a "sixty-five leaper" would combine even five leaping patterns. In fact, there is even a piece sometimes used in practice on the 8x8 board called a root-50-leaper, which fits the naming scheme perfectly (it jumps exactly √5̅0̅ units away from the starting square, which can be achieved either as a {5,5} leap, or as a {7,1} leap).
| | | (5) Posted by Kevin Begley [Friday, Jan 4, 2013 22:17]; edited by Kevin Begley [13-01-04] |
@Bojan,
>Though there are indeed many inconsistencies, I cannot agree that the ones you mention are particularly good examples.
If you are aware of a better illustration of fairy chess disorganization, please, do share.
The one I presented (inconsistencies in units called threeleaper, fourleaper, and fiveleaper) is a fabulous example (and one of many)!
>Namely, the movement pattern of Chinese pieces (leo, pao, vao...) is derived from the game called xiangqi (a Chinese variant of chess).
I have no debate with any of the Chinese units -- they are clear and consistent!
Perhaps you misunderstood that I only encountered a gross example of inconsistency (with some leapers), when searching for the rules for the Chinese pawns.
>In that game there is also a piece (called a soldier) that is an analog of a chess pawn, and the movement of the fairy piece Chinese pawn discussed here is actually derived from the movement of a soldier.
Not quite correct, Bojan.
Our pawns were not derived from those in Chinese Chess.
The movement of a chess pawn, and xiangqi soldiers, is based upon a common ancestor (the Persian game Shantraj, which seems to have been derived from Indian game, Chaturanga).
>It seems to me that your argument about "n-leapers" also misses one point. Namely, "n-leaper" is a piece that may jump exactly n units from the starting square (measured from center to center).
No. This is way off.
First, Leapers should not be associated with a distance -- it is not their fundamental characteristic.
Fundamentally, a leaper has two components (or three/n-components, in the case of 3D/nD chess).
You seem to be confusing the standard Leaper type (alfils, fers, Knights, etc) with a small sub-class of distance-based leapers (e.g., the "Rootfifty Leaper" which is really just a combination of {5,5}Leaper+{1,7}Leaper).
If you want to associate Leapers according to distance, call them all Root-n-Leapers!
If this was the key component, why would mayhematics not define all leapers according to this?
Instead, it inconsistently defines ALL leapers (including even the rootleapers, after having inconsistently dropped the names) according to a coordinate pair!
>That is way threeleaper and fourleaper have only one possible leaping pattern (because that is the only way that puts them exactly three, respectively four squares away from the starting square), while fiveleaper has two possible leaping patterns (in both of them he ends the jump exactly five units from the starting square).
I understand, but this should be called a root25Leaper, not a "fiveleaper."
Leapers are not defined according to the distance they travel.
See the website. http://www.mayhematics.com/v/gm.htm
Note that he defines: "DOUBLE-PATTERN LEAPER One capable of leaps with two different coordinates. fiveleaper, king, rootfiftyleaper..."
If distance is fundamental, the fiveleaper (and the King) would have no double-pattern!
Reread what you stated (above) -- you say: the fiveleaper has two (leaping) patterns.
Why two?
If the pattern were based upon distance (as you suggest), then your position would be that it has a singular pattern (based upon distance)!
You already conceded my point -- it has TWO leaping patterns, because the vector coordinate-pair, not the distance, are the fundamental measure of a Leaper.
I understand that you're playing "devil's advocate" here; but, this is just the tip of an inconsistent iceberg.
Defending fairy chess conventions is currently an exercise in futility (read: fertile ground for future lawyers, and politicians).
>In fact, there is even a piece sometimes used in practice on the 8x8 board called a root-50-leaper, which fits the naming scheme perfectly (it jumps exactly √5̅0̅ units away from the starting square, which can be achieved either as a {5,5} leap, or as a {7,1} leap).
Read what you said.
You said "ROOT-50-Leaper."
You did not say "fifty-leaper."
Do you now see the inconsistency?
threeleaper, fourleaper, fiveleaper, ... Hey, why did you suddenly add the ROOT prefix to the fiftyleaper?
ps: I am beginning to believe that inconsistencies in fairy chess are an intentional counter-intelligence effort.
I'm sure that sounds as crazy as Bobby Fischer; nevertheless, I find legitimate support to the theory, in a consistent pattern of disorganization, on a scale that only intentional deception could produce.
I'll not speculate on the motives -- except to suggest that it may lie deep within the subconscious mind (our shadows).
And, before you laugh out loud, remember: this mayhem was brought to you by people with highly organized, highly logical, mathematical minds.
Mayhematics is an apt title (if you want to hide the truth in daylight).
I will concede that mathematics was fraught with similar inconsistencies.
Archimedes defined Pi quite poorly (c/diameter, instead of c/radius -- radius provides a better fundamental).
When Descartes originally published his coordinate system, it did not even have an orthogonal axis.
Unless you're Fermat, mistakes will happen.
But, fairy chess is doggedly slow to honestly, objectively admit its mistakes.
There's hope for progress -- if fairy chess would institute some mechanism to encourage improvements (like math does); but, this requires a willingness to make consistency the highest priority.
The highest priority in fairy chess, it would seem, is to preserve our own bad legacy -- where elements are dubbed (as if by some divine right), and the names originally given are highly immune to any rational challenge.
| | | (6) Posted by Bojan Basic [Friday, Jan 4, 2013 23:47] |
QUOTE
I have no debate with any of the Chinese units -- they are clear and consistent!
Perhaps you misunderstood that I only encountered a gross example of inconsistency (with some leapers), when searching for the rules for the Chinese pawns.
It seemed to me that you're challenging the name "Chinese pawn" (since the movement of this piece bears no similarity to the movement pattern of the other Chinese units). My misunderstanding, sorry.
QUOTE
Our pawns were not derived from those in Chinese Chess.
The movement of a chess pawn, and xiangqi soldiers, is based upon a common ancestor (the Persian game Shantraj, which seems to have been derived from Indian game, Chaturanga).
I said nothing about the movement of a(n orthodox) chess pawn; I was talking about the movement of a Chinese pawn.
QUOTE
Read what you said.
You said "ROOT-50-Leaper."
You did not say "fifty-leaper."
Do you now see the inconsistency?
threeleaper, fourleaper, fiveleaper, ... Hey, why did you suddenly add the ROOT prefix to the fiftyleaper?
I said (well, not really I but whoever invented the piece, but that's not the point) "ROOT-50-leaper" because it is much shorter than "7.0710678118654752440084436210484903928483593768847-leaper" (and the latter name is not even correct, nor could ever be correctly written this way, from a numerical point of view). I cannot say "fifty-leaper" since that would mean something completely different (that would be a leaper that ends its leap fifty units away from the starting square, while a "root-50-leaper" ends its leap slightly more than seven units away). In fact, let us look at the following quote of yours:
QUOTE
I understand, but this should be called a root25Leaper, not a "fiveleaper."
You are aware that √2̅5̅ = 5, are you? How came that somebody like you, who so strongly and persistently argues that everything should be unified etc., suddenly believes that expression that involves the number "five" should mean one thing, but when the number "five" in the very same expression is replaced with "root-25", it should mean something else?
It seems that it is not me who is playing the devil's advocate here.
| | | (7) Posted by Nikola Predrag [Saturday, Jan 5, 2013 01:28]; edited by Nikola Predrag [13-01-05] |
Kevin probably has in mind some fairy condition where the distance could be minus 5 as a root of 25. For example
w:Ka5,Pa6,"root-1-Leaper"b8;b:Ka7; #1
1."root-1-Leaper"b8-b7+? Ka8!
1."root-1-Leaper"b7->b8#
All pieces on the board are draged one square upwards (except "r-1-L"), a negative move/distance?! :)
| | | (8) Posted by Ian Shanahan [Saturday, Jan 5, 2013 04:40]; edited by Ian Shanahan [13-01-05] |
I agree with Kevin. Some whole-numbers can be represented by more than one Pythagorean triple (there was an article on this subject in "Die Schwalbe" some years ago), so for consistency's sake it would be better to refer to ALL such leapers either as root-n-leapers or {x,y}-leapers (the latter particularly when only one type of leap is possible or desired). A "fiveleaper" is too ambiguous a terminology: it could be a {0,5} or a {3,4}-leaper - or both ... because 5 = root-25 = root-(3^2 + 4^2) = root-(0^2 + 5^2).
| | | (9) Posted by Kevin Begley [Saturday, Jan 5, 2013 09:22] |
@Bojan,
>I said nothing about the movement of a(n orthodox) chess pawn; I was talking about the movement of a Chinese pawn.
My apologies, I misread your comment.
I see now that you were referring to Chinese pawns, in the context of Fairy chess.
>>I understand, but this should be called a root25Leaper, not a "fiveleaper."
>You are aware that √2̅5̅ = 5, are you?
I'm aware that your equality is mathematically correct, yes; and, although a good engineer might quibble about significant digits, I award you full credit.
The issue in question is not the equality, but the form of the expression (the semantics).
One-half-dozen might equal 6.00000, mathematically; but, the two forms may express something entirely different.
Root25leaper would clearly convey that it is based upon a distance calculation (of 5), whereas "fiveleaper" conveys nothing of the sort (only ambiguity).
Furthermore, have you noticed that nobody (including the website in question) refers to other leapers according to their travel distance?
As I pointed out, the website clearly states that root50leapers have a "double leap pattern."
You essentially stated the same, yourself -- which suggested to me that you were only playing devil's advocate.
If people really believe that distance traveled is the fundamental component of a leaper, why do they always resort to the coordinate vectors, when considering/describing leap patterns?
If we are going to be consistent, let's be fully consistent.
We don't label all leapers as root-n-leapers -- why not?
>How came that somebody like you, who so strongly and persistently argues that everything should be unified etc., suddenly believes that expression that involves the number "five" should mean one thing, but when the number "five" in the very same expression is replaced with "root-25", it should mean something else?
I am persistent about consistency -- yes, that's me!
Five conveys something very different than root-25 does -- mathematical equivalence is hardly a valid argument for a semantically inconsistent nomenclature.
If one must be "root50", the other must be "root25" (for consistency, and for clarity).
>It seems that it is not me who is playing the devil's advocate here.
Well, to some degree, we both are -- because, I don't think either of us genuinely cares what somebody dubs this unit. I don't expect any of these "dubbings" will endure -- only the movement patterns.
Last I counted, there are half-a-dozen (note: I am not saying 6.00000) movement rules for the fairy chess unit dubbed "elephant."
Doesn't matter which name sticks -- so long as it is not deliberately inconsistent.
What I genuinely do care about, and advocate for, is more clarity and consistency.
Just so you don't interpret this incorrectly -- I greatly value the many contributions that George Jellis has made to fairy chess, I am thankful for his website, and I've long been a fan of his problems.
A challenge to the semantic consistency of some names referenced on his website is nothing more than an attempt to improve (something we should all welcome).
I don't imagine he (or anyone) is heavily invested in the name "fiveleaper."
I happen to think that a generational opportunity was missed, many years back, to unite variant chess players, programmers, and fairy problemists around a logical, concise, international language, for unorthodox chess elements.
The confusion (which could have been alleviated) only propagates; and, this does detract -- I think significantly.
| | | (10) Posted by Kevin Begley [Saturday, Jan 5, 2013 09:35]; edited by Kevin Begley [13-01-05] |
@Ian,
I vowed never to invoke star trek chess; but, now I'm going to break that sacred oath, just to ask to glaringly obvious question: just how well does a root-50-leaper translate onto a 3-dimensional chessboard?
Of the primitively dubbed "fiveleaper," I'm betting Mr.Spock would say, "His pattern indicates two-dimensional thinking."
| | | (11) Posted by Ian Shanahan [Saturday, Jan 5, 2013 10:35]; edited by Ian Shanahan [13-01-05] |
In general, a root-k-leaper's movements in n-dimensional chess are governed by the number of Pythagorean (n+1)-tuples that define k^2.
e.g. in 3 dimensions, a root-50-leaper could move (3,4,5) as well as (5,5,0) and (1,7,0).
| | | (12) Posted by Kevin Begley [Saturday, Jan 5, 2013 10:38]; edited by Kevin Begley [13-01-05] |
@Ian,
Thanks for sharing information about this issue.
Though I have not yet read the article, I think a succinct case can be made to discard distance as a mechanism to describe leapers, as follows:
If distance were the fundamental component of a leaper, there would be no way to disambiguate the root-25-leaper's two vector components (namely {3,4} and {5,0}).
Bye bye antelope!
However, when leapers are represented by their fundamental vector components, one can succinctly describe the {3,4}Leaper (Antelope), the {5,0}Leaper, and the combinatorial sum ({3,4}Leaper+{0,5}Leaper, or root-25-leaper).
Incidentally, I would refer Bojan to "http://olive-gui.googlecode.com/svn-history/r26/trunk/conf/fairy-pieces.txtbucephale"; (or just read popeye's py-engl.txt file) where this IS called "root-25-leaper" (aka bucephale).
So, it seems many others have arrived at the same conclusion: while root-25 = 5 mathematically, the two expressions are semantically different!
The failure of distance description should have been realized, and quickly discarded.
| | | (13) Posted by Ian Shanahan [Saturday, Jan 5, 2013 14:18]; edited by Ian Shanahan [13-01-05] |
@Kevin. Your link didn't work (at least on my computer!); this one does:
http://code.google.com/p/olive-gui/source/browse/trunk/conf/fairy-pieces.txt?r=26#29
| | | (14) Posted by Hauke Reddmann [Saturday, Jan 5, 2013 16:17] |
@Kevin: I agree that a fiveleaper should mean (5,0) and that a
(5,0)+(4,3) leaper should be called root25-leaper...in German
("Wurzelspringer") this is common notation anyway, AFAIK.
I disagree, though, that the one is "more fundamental" than the other.
This depends on whether you see distance or direction as more
fundamental. My other half is mathematician, thus I refuse that
issue as a mere rule-of-math-play. You can choose it as you like,
like the axiom of choice.
OK, so what is the more "easy" way to build the movements of all
chess pieces, fairy included, from scratch? That's another can of
worms, and here I probably would plea xy coordinates have the right of way.
But still, what's the point of defining the root25 as (5,0)+(4,3)
instead of root25?
Hey, I can't count how many rounds of fisticuff I exchanged with
Wieland Bruch because I think that the historically grown system
of White Line Combinations is an illogical kludge! But as kludges go,
it's easy, it's patchable, it's understandable, it *works*.
Hauke
| | | (15) Posted by Kevin Begley [Saturday, Jan 5, 2013 21:28]; edited by Kevin Begley [13-01-05] |
@Hauke,
>I disagree, though, that the one is "more fundamental" than the other.
This depends on whether you see distance or direction as more
fundamental.
Hauke, it's not a question of distance versus direction.
It is a question of an omni-directional vector (expressed as a coordinate pair), versus a mere direction.
The o-d vector can describe any leaper (in the language of math, this forms an orthogonal basis, and can be used as a valid axis to describe all n-dimensional leapers).
If you want to express an antelope, the o-d vector works: (3,4).
If you want to express a root-25 leaper, a sum of the o-d vector works: (0,5) + (3,4).
If you want to expand dimensions, to express 3D units, you simply add a third component (which is zero for all 2D units).
Using direction alone, you can not express the movements of all leapers -- even in the 2-dimensional plane.
Direction does not form a basis, and can not be used as a valid axis for all leapers!
Proof:
By distance alone, you can express the Root25-Leaper's movement -- quite simply: d=root25, or d=5.
However, it is impossible to express an antelope's movement pattern (3,4) -- here the distance is also 5, but d=5 yields an additional component: (0,5).
Using only distance, you can never express the antelope's movement pattern.
Using coordinates (as an o-d vector expression), you can describe any leaper.
Distance is not the fundamental description of leapers, and any naming convention which is based upon non-fundamentals must assume the burden of avoiding confusion.
The fanciful naming convention I've noted here (threeleaper, fourleaper, fiveleaper) was not so careful; and, it resulted in considerable confusion.
The best remedy is to apply the "root" prefix convention to the "fiveleaper" (to obtain the "root25L").
The "root-n-leaper" is a fine naming convention (it clearly describes a distance component, and suggests the two o-d vector components), providing it satisfies two criteria:
1) root-prefix can ONLY apply to leapers which can be fully described by distance, and
2) root-prefix can NEVER apply to leapers which can be described more fundamentally, by a single coordinate.
The root prefix can not be applied to the fundamental leapers, which can be described by less than two o-d vector (coordinate) components, or the resulting convention yields another (equal but opposite) semantics failure.
The "threeleaper" can not be called "root9leaper" -- because it would similarly lead to confusion, and wreck a logically coherent convention (which was intended to be based upon fundamental elements).
That's why it is important to describe the most fundamental units first (contrary to the historical evolution of fairy chess)!
If we simply define the fundamental elements first, it becomes immediately apparent why secondary elements (like the "root25") are burdened to follow a primary convention (and we can generally avoid bad conventions, before they begin).
In fairy chess, bad conventions propagate like an ubi-ubi on orphan-sentinels.
We need to impose haan, and rundlauf to square one.
| | | (16) Posted by Kevin Begley [Saturday, Jan 5, 2013 21:43]; edited by Kevin Begley [13-01-06] |
@Nikola,
>"Kevin probably has in mind some fairy condition where the distance could be minus 5 as a root of 25.
Actually, I do have in mind a fairy unit: the "Root(-1)Leaper."
Movement pattern: it can leap into the imaginary plane; and from the imaginary plane, it can leap back.
Much like a Zero ({0,0}Leaper -- not to be confused with a Dummy{no moves}) would move in Alice, except that the captures are made on the alternate board. In Alice, a Zero can never capture.
Essentially, this suggests an Alice variant -- and, I think perhaps imaginary components might be a preferred way to describe Alice movements!
With imaginary components, the riders can be described such that they ride across two boards.
For example, a Ra1 (on board A) could ride to b1(B)...c1(A)...d1(B)...e1((A)...f1(B)...g1(A)...h1(B).
This leaves a monochrome impression for Rook moves viewed from each plane (same is true for Nightriders -- indeed, any alternating color rider appears monochrome, alternating on both boards. Bishops, of course, are always monochromatic)!
Leapers would capture onto the alternate board.
Hoppers would ride across two boards, such that if they encounter a hurdle on A, they leap it to land on B (possibly capturing on B).
Checks in Alice are resolved differently, however; here, checks would be resolved according to the final position.
A king could step into check on board (A), providing it does not land in check, after completion of the move.
I believe imaginary components should provide an orthogonal basis to fully describe all possible moves, and transfers into the imaginary (Alice) plane.
I actually just thought of this as a joke, but was surprised to find no such Alice variant listed (here: http://en.wikipedia.org/wiki/Alice_chess).
Presuming this is not anticipated, it seems quite interesting -- and, if original, I'd certainly welcome composers to help provide some example problems (retros would seem particularly interesting -- René Millour, are you listening?).
ps:
To determine whether you can castle through check, I always prefer to resort to virtual moves (step there and see).
If you can castle, you might get different results (depending how you consider the dynamics of the castling move).
I prefer to consider castling as a K-ride(0,2) + R-tunneling-ride(ride through K), which would yield.
white 0-0 (from A): wK arrives on g1(A), wR arrives on f1(A).
white 0-0-0 (from A): wK arrives on c1(A), wR arrives on d1(B!).
If you prefer to consider the R-slide to be a hopper over the K, the hop would fail in short castling.
Double-steps of pawns, I expect, must be considered a ride, not a leap (because en passant depends on stepping onto the intermediary square, which leaps -- save decomposed leaps -- can not do).
This is the real trouble with special case moves -- they are not well defined, in terms of the most fundamental descriptions of unit movements (leaps, rides, hops, etc).
How exactly does one model the castling move, or double-step pawns moves (based upon fundamental movements)?
If we can't answer these questions definitively, it proves that our foundation is broken!
| | | (17) Posted by Sarah Hornecker [Saturday, Jan 5, 2013 22:05]; edited by Sarah Hornecker [13-01-05] |
QUOTE
In fairy chess, bad conventions propagate like an ubi-ubi on orphan-sentinels.
We need to impose haan, and rundlauf to square one.
 (= 1+1 ) (= 1+1 )
Selfstalemate in one
1.h8 royal kamikaze 0,7 vertical only leaper that can't be given check.
1.-h1 any, stalemate (capturing is illegal because of kamikaze)
What do you mean, this is not allowed?
EDIT: Corrected! Thanks, Kevin! :-)
| | | (18) Posted by Kevin Begley [Saturday, Jan 5, 2013 22:15]; edited by Kevin Begley [13-01-05] |
Siegfried,
Busted, 1...h1=R/Q/vertical-only(0,7)Leaper # (all non-royal, but kamikaze may be optional)!
| | | (19) Posted by Nikola Predrag [Saturday, Jan 5, 2013 23:12] |
Of all these precise and exact fairy semantics and mathematics I've learned that 5=root25=-5
| | | (20) Posted by Kevin Begley [Saturday, Jan 5, 2013 23:17]; edited by Kevin Begley [13-01-06] |
Haha! Nikola!!
I hereby nominate your last for best comment of the year, 2013.
It may be early yet, but I like your odds!
Deduct 5 points from me and Bojan, for failing to recognize that: root(25) is not mathematically equivalent to 5.
And, now that this is established, it offers a mathematical reason (beyond semantics) why the "root25Leaper" is not the same as the "fiveleaper."
| |
Read more... | Page: [Previous] [Next] 1 2 3
MatPlus.Net  Forum Forum  General General  Chinese Pawns Chinese Pawns |
|
|
|
 ISC 2024
ISC 2024 Forum
Forum  General
General  Chinese Pawns
Chinese Pawns