Website founded by
Milan Velimirović
in 2006
23:29 UTC


| |
MatPlus.Net  Forum Forum  General General  Computers & chess problems ? Computers & chess problems ? |
| |
|
|
|
|
You can only view this page!
| | | (1) Posted by [Thursday, Apr 3, 2008 16:08] | Computers & chess problems ?
I've just stumbled on an odd-looking article by Yaakov HaCohen-Kerner et al.,
Jerusalem College of Technology: 'An Improver of Chess Problems', published
in 1999 in the journal 'Cybernetics and Systems'.
I have just begun to read it ... and about when I read
"In this paper, we propose a model that is capable of improving
some of the existing chess problems. We have formalized a major part
of the knowledge needed for judging the quality of chess problems. The
basic idea is to attempt to improve a given problem and its solution by a
series of meaningful chess transformations using a hill-climbing search,
while satisfying various criteria, step by step, until no further adequate
transformations are available."
that it strikes me that there should have been some kind of evaluation
in problemist circles. The authors claim to have found improvements
(only under the rules they formalized, of course) to about a third of the
problems they tried it out on.
Now ... has anyone here read this? Can anyone comment on it? (My first impression
is that it looks as if they've started from M.O.E., but I can't find that
in the references.) The chess problem experts involved seems to have been
Josef Retter and Jean Haymann.
I see that there is a follow-up article from 2006, from the same principal
author, but I haven't looked at that yet.
| | | (2) Posted by Vladimir Tyapkin [Thursday, Apr 3, 2008 18:07] |
In the abstract to the second article they claim to improve 89% of problems, from the same sample of 36 known problems, some significantly. If you have access to the full article(s) is there any example of such 'improvement'? One can pay $35 and read the whole article but I am a bit skeptical.
| | | (3) Posted by Frank Richter [Thursday, Apr 3, 2008 19:08]; edited by Frank Richter [08-04-03] |
I found on my hard disk a PDF by Fridel Fainshtein labeled "An Orthodox k-Move Problem-Composer for Chess Directmates". The work was supervised by Dr. Yaakov HaCohen-Kerner and other people.
The PDF is available for downloading here: http://www.problemschach.de/KMOVEComposer.pdf
In the file you can find some examples of the improvements (p. 68ff.). Hope this can help.
| | | (4) Posted by Vladimir Tyapkin [Thursday, Apr 3, 2008 19:35] |
Frank, your link does not work.
| | | (5) Posted by Frank Richter [Thursday, Apr 3, 2008 19:44] |
A "C" was needed, now it works, sorry!
| | | (6) Posted by [Thursday, Apr 3, 2008 20:45]; edited by [08-04-03] |
After reading through it a couple of times, as well as the follow-up, it
seems it has less with chess problems to do than with searching for better
solutions in a complex search space.
There's a scoring function applied to a position and its solution, rather along
the lines of M.O.E.: 10 points for a miniature, 10 point if Black king is the center
of the board, 3*piece value for pinning key move, and so on. They never refer to
M.O.E., though, which robs the reader of a possibly interesting comparison of evaluation
functions.
There's also a transformation procedure to find new positions from old:
remove a piece, add a piece, replace bishop with queen and vice versa,
also rook<-->queen, move position horizontally and vertically, and so on.
Then generate as many 'new' positions as possible (well, almost) by
repeated application of these rules, check that they still are single-key
two-movers, then score them: the highest scored position 'wins'.
The test was limited to 36 problems -- and in most of them no improvement was found.
The problems are said to have been collected from Harley's book on two-movers,
three of Howard's books, and an series of articles on composing by Haymann
in Variatim.
The second paper adds some ingenuity to the search, and some new motifs to
score.
Example 1: (remember, two-movers)
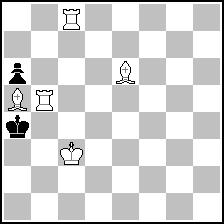 (= 5+2 ) (= 5+2 )
Original problem
 (= 4+2 ) (= 4+2 )
Improvement found in first paper
 (= 5+3 ) (= 5+3 )
Improvement found in second paper
Example 2:
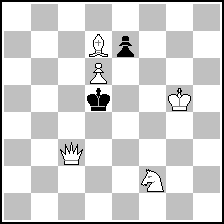 (= 5+2 ) (= 5+2 )
Original problem
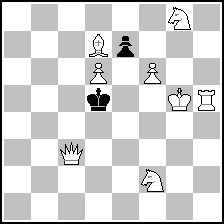 (= 8+2 ) (= 8+2 )
Improvement found in second paper
There's also an explanation what it is that actually makes the improvement:
of course, it depends entirely on the components of the scoring function,
and how highly a pickaninny or a Grimshaw is rated. In the second example,
it's pretty clear that the loss of miniature form is not considered as important
as the added features.
If a reasonably good scoring function could be found, though, it seems
as if it would be possible to enter a half-good, possibly even faulty,
problems, and then get a list of possible improved diagrams to choose from
-- the formal correctness will be there.
Added: Fridel Fainshtein, mentioned in other posts, is the co-author of
the second paper from 2006.
| | | (7) Posted by Juraj Lörinc [Friday, Apr 4, 2008 09:42] |
Well, these Bytes are delicious. Thanks, Frank & Anders.
| | | (8) Posted by Hauke Reddmann [Friday, Apr 4, 2008 15:19]; edited by Hauke Reddmann [08-04-04] |
Very interesting. I claim to have an instinct that allows
me to judge with just a glance on a problem (assuming
that solution, and more important, full theme is given)
if the material might be improved. If you read your
GödelEscherBach, instinct is cheating :-) - I follow rules
that could be formalized. (E.g. material that is just needed
for cookstopping usually is the first to walk the plank.)
So, it would be interesting to throw the program at actual
problems I improved. Here is a very recent example:
Michael Keller (#3366, Schach-Aktiv 1/2008)
 (= 9+10 ) (= 9+10 )
1.Nf4~ (2.Rxg5#) 1.-Bxc1!
1.Se6? Bxc1, Bd5 2.Sxd4, Re5#, but 1.- Td5!
1.Se2? (2.Rxg5#) Bxc1, Rd5 2.Sxd4, Qe6#, but 1.- Ld5!
1.Sd5! (2.Re5/Qe6#) Rxd5, Bxd5, Qxe4 2.Qe6, Re5, Rxg5#
Observe: The bQ stands unfortunate, if moving it to the file of the wRR works,
bPf2g3 immediately bite the dust. Oh, the Pd4. Is that a problem? No, the bQ can
also take the function of the bBc1 too! Another two pieces drop off.
Move everything to the border for the needed space. So much for the new matrix,
now fine tuning begins. The more multiple functions pieces take, the better. Result:
Michael Keller, version Hauke Reddmann (#3366a, Schach-Aktiv 3/2008)
 (= 8+7 ) (= 8+7 )
Little immaterial improvements:
- The bQ now has 2 thematic variants.
- The wQ is used a bit better with an additional mate on b2 after 1...Rc1.
- No white pawns.
(BTW still no justification to put a "HR after MK" on the diagram :-)
Hauke
| | | (9) Posted by Paz Einat [Monday, Apr 7, 2008 13:52] |
I browsed through the PDF paper through the link given by Frank.
All examples I have seen are Miniatures turned into something more complex. It is nice to have an algorithm that can do this. However, the point in miniatures if to express the most by a maximum of 7 pieces. Adding some pieces and increasing complexity is not an issue at all and an insignificant achievement in itself.
I am impressed with Hauke's improvement of Kellers problem. Well-done! So the question is whether those algorithms can undertake such a task to arrive at the best position for such a specific combination.
| | | (10) Posted by Hauke Reddmann [Monday, Apr 7, 2008 14:15] |
Yes, this is exactly the question I would ask too. For a moment put
aside that you can ruin a theme with the slightest construction
detail and assume a composer could now routinely throw his problem into
the computer first for optimization, putting me out of business :-)
(I *won't* name names who especially would profit :-))
Would that be a bad thing, meaning any dummy could compose now?
Would it be a good thing, meaning the primate of idea over form?
(I'd love to have had such a program 20 years ago when I still was
full of ideas but lacked the technique - I may be able to compose
any composable theme in five minutes now but that ability took me
20 years of study!)
Hauke
| | | (11) Posted by Neal Turner [Monday, Apr 7, 2008 16:06] |
All this begs the question of what composing is really about?
If it's just about producing chess problems then the computer is a great tool, and an Automatic Problem Generator is the logical answer.
However if it's about the process of composing then the computer is a mixed blessing.
I suppose most composers have had the experience of the computer coming up with variations or solutions which are surprising, and may be more interesting than the composer's own ideas.
This has happened to me a number of times and has resulted in published problems, but mostly these problems leave me feeling flat compared with those were the content is my own.
The real joy of composing - at least for me - are those Eureka! moments which appear all too rarely.
But these can only come from one's own efforts and never from the computer no matter how original and exciting the lines it throws up.
| |
No more posts |
MatPlus.Net  Forum Forum  General General  Computers & chess problems ? Computers & chess problems ? |
|
|
|
 ISC 2024
ISC 2024 Forum
Forum  General
General  Computers & chess problems ?
Computers & chess problems ?