|
|
| (1) Posted by Hauke Reddmann [Tuesday, Aug 14, 2007 11:04] |
A little construction problem for you
You all know material doesn't neccessarily count (man Immortal Game),
but what is the extreme?
A position White can't win even if he has maximum advantage.
Since that is still a bit easy, let's make it more precisely.
- Black has only the king.
- White has as many as you are willing to give him, so don't care
about legality, use 50 queens if you can :-)
- Neither side is stalemated. White can repeat moves or stalemate
Black on each move, but that's all he can do.
I think I once published this in the SCHWALBE, but not with enough
precise a wording :-)
Hauke
|
|
| (2) Posted by Dmitri Turevski [Tuesday, Aug 14, 2007 17:25] |
Does this fit (52 queens)?
 (= 61+1 ) (= 61+1 )
|
|
| (3) Posted by Sarah Hornecker [Tuesday, Aug 14, 2007 17:41]; edited by Sarah Hornecker [07-08-14] |
I believe, my solution (originally sent to HR via note on 13:34 and 15:24) is better!
 (= 61+1 ) (= 61+1 )
PS, 17:43: Thinking again about it, I prefer this one, but only if it is white to move:
 (= 62+1 ) (= 62+1 )
Instead of Sb1, a bishop could be used as well.
If it doesn't matter, who is to move, the setting above seems the best
|
|
| (4) Posted by Dmitri Turevski [Tuesday, Aug 14, 2007 18:04]; edited by Dmitri Turevski [07-08-14] |
Sure, it has 4 more white queens :) However, giving the bK more freedom is funny too, eg:
 (= 33+1 ) (= 33+1 )
here white can both repeat moves or stalemate (or be stalemated)
Updated:
On a second thought it seems like more play can be added. This looks like a draw too (white to move):
 (= 33+1 ) (= 33+1 )
1. f8Q/B stalemate
1. f8N Kg7 2. ~ K:f8 and there's no possible mate (even if white forces bK to move to a8 or h1)
1. f8R Kg7 2. Rf7+ Kh8 3. Rf6(f8) Kg7 repetition
1. Kc3 Kg7 2. Kd4 Kf8 3. Ke5 Kg7 4. ~ Kf8 white king can't win a tempo on a checkers board and rook promotion is secured by bK blocking f8.
Am i correct?
|
|
| (5) Posted by Sarah Hornecker [Tuesday, Aug 14, 2007 21:04]; edited by Sarah Hornecker [07-08-15] |
The first position above was well-known but on the second position you added a very nice point. I wonder if a real study can be made with this?
PS: 2...Kf8 should gain an exclamation mark, since white would win after 2...Kh8:
3.f8R Kg7 4.Rf7+ Kh8 5.Rf6 Kg7 6.Ke5
|
|
| (6) Posted by Dmitri Turevski [Wednesday, Aug 15, 2007 07:45]; edited by Dmitri Turevski [07-08-15] |
Are you sure that white can win with rook after 6. Ke5 ?
However, the tempo/opposition is not a fake, here's an idea of white play if white king stands on a1 in the initial position:
1. Kb2 Kg7 2. Kc3 Kf8 3. Kd4 Kg7 4. Ke5 Kf8 5. Kf4 Kg7 6. Kg5! Kf8 7. Kh6 Ke7 8. Kg7 ~ 9. f8Q(B)! and win.
Updated: disregard that, please. Black can play 6... Kh8! and now it seems like its draw no matter where (a1/b2) the white king is placed.
|
|
| (7) Posted by Hauke Reddmann [Wednesday, Aug 15, 2007 12:43] |
Interesting position. (I did something similar in the SCHWALBE -
- I proved something to the effect that it already suffices
to remove, say, the Bd7 to make 1.f8S a winning move.)
Note that I stated White *may* stalemate *or* repeat on *any* move,
to make the position relatively unique. It works quite similar to
Siegfrieds construction, just with a little fine tuning.
Hauke
|
|
| (8) Posted by Sarah Hornecker [Wednesday, Aug 15, 2007 15:27]; edited by Sarah Hornecker [07-08-15] |
Ok, my tests say white can't win with the extra rook...
Hauke, stop bothering us until we come up with this:
 (= 60+1 ) (= 60+1 )
PS: See Kostas Prentos' reply below, somehow I must have overlooked this...
|
|
| (9) Posted by Kostas Prentos [Wednesday, Aug 15, 2007 16:09] |
This position allows 1.Qf2-e1, 2.Qe3-f2, 3.e2-e3 and 4.Kd1-e2#
|
|
| (10) Posted by Zalmen Kornin [Wednesday, Aug 15, 2007 16:26] |
THE HAREM PROBLEM (original) Remove 61 Queens for a decent (dual-free) #1 (black to play) - how many solutions?  (= 63+1 ) (= 63+1 )
|
|
| (11) Posted by Dmitri Turevski [Wednesday, Aug 15, 2007 22:53] |
Excuse me please, mr Reddmann, do you mean that in similar position where white has an extra white square to maneuver (i.e. d7) you proved that immediate promotion to knight wins and pulling the white king closer and promoting to rook fails to win? Amazing.
|
|
| (12) Posted by Hauke Reddmann [Thursday, Aug 16, 2007 12:16] |
I stand corrected:
1. White kicks out bK by opposition and promotes to R:
No idea if the position is won. Let's all analyze how
many B must be removed to make it so!
2. White kicks out bK by oppostion and promotes to S:
Sorry, I botched up again. With *two* free white
squares the position is won. See here
http://www.hackerhost.info/hosting/user/Hauke/loesung.html#S11467
for the mating algorithm.
I won't exclude the possibility that *one* is enough,
but doubt it. Sorry for the confusion.
Hauke
P.S. I had this is mind (+51wQ which I'm too idle to input :-)
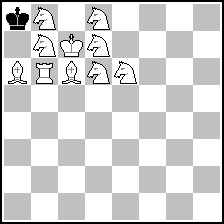 (= 10+1 ) (= 10+1 )
|
|
| (13) Posted by Kostas Prentos [Thursday, Aug 16, 2007 13:15] |
The position above works only with white to move. If black moves first, there is mate with 1...Ka7 2.Sc8+ Ka8 3.Sbd6#.
If the goal is to have a "positional" draw (not immediate stalemate), it seems that Dmitri Turevski's position in post No.2 becomes optimal with the replacement of the white pawns (b2 and g2) by knights.
If the immediate stalemate is acceptable, then Siegfried Hornecker's positions in post 3 are fine.
|
|
| (14) Posted by Dmitri Turevski [Thursday, Aug 16, 2007 13:55] |
Rook with 2 "holes" doesn't win, i believe. There are quite a few types of mate positions and it seems that they all don't have a legal retro-play. Nice little supplement to your algorithm (unfortunately, i couldn't follow it - diagrams are not displayed, but the idea of the knight becoming a very powerful piece on such a board is great).
With 3 "holes" there's a helpmate (wKg5, wRh4, bKf7, holes: h5, g6, h7; 1.Kg7 Kh5 2.Kh8 Kg6#).
|
|
| (15) Posted by Hauke Reddmann [Friday, Aug 17, 2007 11:05]; edited by Hauke Reddmann [07-08-17] |
You mean bKf8, surely.
The rook is extremely clumsy on this board, but with my
combined OTB/problem power :-) I soon found a way how White
might avoid stalemate and jettison the blocks, e.g. :
wKe7 Rh4 sKg7 *g8 h5
1.Rh5 Kh8 2.Bhg8+ Kg7 3.Rh7#
In the "wrong corner" you need one hole more. And since you
could park the holes somewhere strategically, and drive the
bK to the border by opposition, using the R to block the
emergency exit, we might conclude:
- R + 3 holes are won
- R + 2 holes is won if we find a way to kick Black out of
the wrong corner (without letting him head straight to the
other). Quite reminiscent of KBS/K, eh? :-)
Hauke
EDIT: Looks like it *is* possible, by creative use of diagonal
opposition. So I daresay
- R (or S) + 2 holes is won. Now if we only had a Nalimov
table for these endgames :-) (In fact, 3 + 2 pseudo pieces,
at most ~20 moves to analyze...A good programmer could solve
this in a day.)
|
|
| (16) Posted by Dmitri Turevski [Friday, Aug 17, 2007 15:03] |
You are absolutely correct. I must think more thoroughly before i post. I have seen this mate, but somehow completely overlooked that it can be constructed, not to say forced.
|
|
No more posts |
MatPlus.Net  Forum Forum  Retro/Math Retro/Math  A little construction problem for you A little construction problem for you |
 ISC 2024
ISC 2024 Forum
Forum  Retro/Math
Retro/Math  A little construction problem for you
A little construction problem for you