Website founded by
Milan Velimirović
in 2006
19:19 UTC


| |
MatPlus.Net  Forum Forum  General General  Number of all "4 men only" Number of all "4 men only" |
| |
|
|
|
|
You can only view this page!
| | | (1) Posted by Hauke Reddmann [Thursday, Dec 11, 2008 11:06] | Number of all "4 men only"
For simplicity, let's restrict to orthodox n# (since this is,
apart from studies*, the only thing implicitely contained in the
Nalimov tables). Obviously, the number of positions is smaller than
64*63*62*61*5*10. (And this is only the "dumb" approximation,
I'd knew a handful of ways to bring the number down.)
This means it *might* be possible to at least scan all 4 men
positions in the Nalimov and check if the key to shortest
n# is dual-free.
(Yes, an orthodox n# may have more than one solution if
the author insist so. Restrict to orthodox orthodox then :-)
Can it be done?
Should it be done?
What do you expect for the result? Which percentage will
Speckmanns collection already cover?
Hauke
* I have a file with "all" <4 men studies, and I must say,
Longcat is loooooong.
| | | (2) Posted by Dmitri Turevski [Thursday, Dec 11, 2008 15:21] |
I did a similar thing couple of years ago, but abandoned it completely because it is boring (its boring level is over nine thousand). The whole approach looks like a deadend to me because it hits the "total pieces on board" limit too fast. I think, problem composing algorithm should search for combinations of motives/effects and check whether they are feasable rather than analyze ready setups. My pastime is working on it, but i doubt i have something ready soon, not to say ever.
Nevertheless, here's a twomover from my "bruteforce" attempts,
hardly original, but i like it: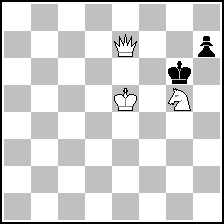 (= 3+2 ) (= 3+2 )
#2*v | 1... h5 2. Qf6#
1. Kf4? zz 1... h6 / Kh6(Kh5) 2. Qf7 / Q(x)h7# 1... h5!
1. Se6! zz 1... h6 / h5 / Kh6(Kh5) 2. Sf4 / Qg7 / Qg5# |
Back to your questions:
>Can it be done?
Yes.
>Should it be done?
No idea.
>What do you expect for the result?
I expect one ending his days digging through the pile of the resulting junk. It is not being dual-free what makes an aestetic value, not at all. I think one should search for more specific patterns like switchbacks, or rundlaufs, or underpromotions to find something interesting in his lifespan.
>Which percentage will Speckmanns collection already cover?
My guess is that it would be a rather small percentage. However, if you manage to leave the junk out somehow, then this percentage can be surprisingly high (i guess again).
| | | (3) Posted by Michael McDowell [Friday, Dec 12, 2008 09:41] |
The diagram adds a worthwhile try to a problem by Herbert Hultberg, Tidskrift for Schack 1928, which starts the white king on e4 and the knight on g7.
| | | (4) Posted by Torsten Linß [Monday, Jan 12, 2009 23:22] |
> Nalimov and check if the key to shortest n# is dual-free.
Why Nalimov? His tablebases are not designed to answer this kind of questions efficiently.
> Can it be done?
No, because there is no definition of a "correct problem".
> Should it be done?
You'll always find somebody who is willing to waste his time on anything...
> Which percentage will Speckmanns collection already cover?
What's Speckmann's collection? A collection of FMO problems?
> What do you expect for the result?
- Have a look at the problems in the collection and you'll know what to expect of problems of this kind.
- Or are you asking for a number?
BTW, do you understand the following problem?
Ke5 Db1 - Kh6 Tc3, #12
1.Db4 Te3+ 2.Kf4 Te8 3.Kf5 Tg8 4.Dh4+ Kg7 5.Dg5+ Kh7 6.Dh5+ Kg7
7.Dg6+ Kf8 8.Df6+ Ke8 9.Ke6 Tg6 10.Df6*g6+ Kd8 11.Dc2 Ke8 12.Dc8#
[Why not Db7 in the initial position?]
| | | (5) Posted by Hannu Harkola [Tuesday, Jan 13, 2009 10:43] |
If Db7 then it is 9# by 1.Kf6.
| | | (6) Posted by Hauke Reddmann [Tuesday, Jan 13, 2009 17:27] |
@ Torsten: Yes, Speckmann did a collection of orthodox FMO. E.g. look here:
https://www.schachversand.de/d/detail/buecher/685.html
Do I understand the #12? Depends on the definition of "understand".
I have ELO 2300 and thus it's no wonder I took a peek into the new
TB defenses in the KQ/KR ending - you'll never know :-) The trick is
to position the Q such that the R can't pester you with checks from
far behind. Thus I understand the "what", but the "how" might still
be above my ELO. (Luckily any game will be either a rapid where the
opponent doesn't have enough time either, or a long game, where I always
have one hour more on the clock - if I make it into the endgame :-)
Hauke
| | | (7) Posted by Kevin Begley [Thursday, Jan 15, 2009 09:24] |
Also, if Db7, there's 1.Qg2! with a trivial mate in 11, which I assume went unstated because of the obvious duals.
| |
No more posts |
MatPlus.Net  Forum Forum  General General  Number of all "4 men only" Number of all "4 men only" |
|
|
|
 ISC 2024
ISC 2024 Forum
Forum  General
General  Number of all "4 men only"
Number of all "4 men only"